Aug 10 Airport Shuttle-Exact Solution

This paper addresses the problem of optimally routing and scheduling airport shuttle vehicles that offer pickup and dropoff services to customers through ridesharing.

Matthew Mohebbi
IT Curves (and Supreme Airport Shuttle, Inc.)
Gaithersburg, MD 20879
Email: mmohebbi@itcurves.net

Revised from original submission Submitted for presentation at the 2014 Transportation Research Board 93rd Annual Meeting and for publication in the Transportation Research Record

Download Article

ABSTRACT

This paper addresses the problem of optimally routing and scheduling airport shuttle vehicles that offer pickup and drop-off services to customers through ridesharing. This problem, which is a version of the Dial-A-Ride Problem (DARP), is formulated as a mixed integer program. An exact solution approach applying constraint programming within a column generation framework is proposed, as well as adaptations of two existing heuristics, for its solution. Implementations of the mathematical program and proposed solution approaches for three different operational policies are presented. Performance of the proposed approaches in terms of computational requirements and solution quality is evaluated on a real-world case study involving service records for one service day out of Washington Dulles International Airport provided by an actual airport shuttle service provider. Results show that the heuristics provide good approximations to the exact solution.

INTRODUCTION

This paper addresses the problem of optimally routing and scheduling airport shuttle vehicles that offer pickup and drop-off services to customers through ridesharing. This work was motivated by a need for tools to support efficient resource management at Supreme Airport Shuttle, Inc. This company provides ridesharing services to customers travelling to/from two major airports in the Washington, D.C. area. In its outbound operations, they have a fleet of vehicles used to pick up customers from the airport’s arrival doors and drop them at customer-chosen destinations. The vehicles also provide inbound services in which they pick up customers at multiple origins outside the airport and drop them at the airport’s departure doors. Customers request services by phone, online or at a kiosk in the airport or hotel. Each request includes information on the number of passengers, pickup location and time, and (or) drop-off location and time. A single request can be for a one-way trip (outbound or inbound) or a round trip (outbound and inbound). Each request results in a trip from the arrival door of the airport to the trip’s destination or from the trip’s origin to the departure door of the airport. Thus, requests can be made in advance or may arise dynamically on the same day of service. One or more trips are served by one vehicle through a route, which is defined by a circuit that is traveled by a vehicle starting from and ending at the holding lot in the airport. Each vehicle may have multiple routes during a shift.

Reduced total passenger-miles traveled resulting from ridesharing and efficiently designed routes can increase profitability of the service provider and aid in diminishing traffic congestion and related negative externalities, including environmental pollution. Thus, an optimization model is proposed for the problem of determining a set of routes and schedules that meet service quality, resource, labor and vehicle capacity constraints while minimizing total cost in terms of vehicular use and total wages in the context of airport ridesharing services. This problem, which is a version of the Dial-A-Ride Problem (DARP), is called the Airport Access Ridesharing Problem (AARP) here.

The AARP is considered under three different operational policies that are illustrated in FIGURE 1. Policy 1 handles outbound and inbound trips separately, assigning different sets of vehicles to each. This policy is under consideration, because in current operations demand for outbound service far outweighs the demand for inbound service. Policy 2 handles outbound and inbound trips simultaneously, permitting a single vehicle to drop off outbound and pick up inbound customers at all points along the route. Under Policy 3, all outbound trips must be dropped off before the same vehicle starts picking up inbound trips. This last policy gives preference to outbound customers, the majority of the company’s actual customers. While one can show that Policy 2 will always produce the most efficient routes for the operator, other policies must be considered under certain contractual agreements or passenger service policies.

The AARP is a difficult combinatorial optimization problem; the number of possible solutions for it grows exponentially with increasing problem size. Even obtaining a single feasible solution by hand can be quite challenging. Yet, efficient use of limited resources is key to providing profitable, quality service that, by contract, meets service level agreement requirements. Thus, for real-world problem instances, tools to support the identification of feasible and optimal or near-optimal solutions can be crucial. An exact solution algorithm and two heuristics are proposed to solve the AARP. The exact solution applies a Constraint Programming based Column Generation (CPCG) approach (1). The first heuristic is a variant of the sequential insertion heuristic proposed by Jaw (2) for a related dial-a-ride problem (DARP). The second is adapted from Solomon’s work on the Vehicle Routing Problem with Time Windows (3). Performance of the proposed heuristics is compared in a case study involving data from one day’s operation of the Supreme Airport Shuttle fleet at one airport. The solution approaches were implemented and adapted to the three operational polices. Results from runs of the algorithms are analyzed and compared based on a variety of performance measures.

RELATED LITERATURE

The AARP shares several characteristics of a variety of established optimization problems. First, the AARP is related to the Vehicle Routing Problem with Time Windows (VRPTW) (4). In the VRPTW, a vehicle must arrive at each customer within a given time window. Where soft time window constraints are permitted, a penalty for early or late arrival may be incurred. For comprehensive reviews of optimization algorithms for VRPTW, the reader is referred to (6-9). The AARP similarly has time windows; however, these constraints are hard. Thus, any solution that violates these constraints is infeasible. The AARP differs from the VRPTW by also including maximum ride time constraints needed to control the time spent by each passenger traveling in the vehicle, as well as maximum shift durations. Moreover, customer stops are paired in the AARP, since each customer has a pair of pickup and drop-off locations, and the pickup must be completed before the drop-off. This creates additional precedence constraints. Such pairing and precedence of customers are captured in a generalization of the VRPTW, the Pickup and Delivery Problem with Time Windows (PDPTW) (10).

As in the AARP, in the PDPTW the origin of each request must precede its destination on each vehicle tour, and both locations must be visited by the same vehicle. Among the PDPTWs in the literature, those that address the DARP (2) are most relevant. Comprehensive surveys of optimization algorithms on the PDPTW are provided in (11) and (12), and on the DARP in (13) and (14). The DARP involves passenger transportation between paired pickup and delivery points and takes user inconvenience into account. The AARP can be viewed as a special case of the DARP with one-to-many and many-to-one operations. See (15) for a discussion of this variant for a single vehicle. The AARP with Policy 1 or 2 can be treated as a PDPTW; however, operational Policy 3 requires that inbound movements not begin until outbound movements are complete. This variant does not appear to have been addressed previously.

The Vehicle Routing Problem with Backhauls and Time Windows (VRPBTW) specifically captures the one-to-many and many-to-one characteristics of the AARP. The VRPBTW involves linehaul and backhaul operations. In the linehaul operations, the loading of goods onto a vehicle is completed at one or more depots, and goods are transported to one or more destinations. In backhaul operations, once linehaul operations are complete (or partially complete), goods are loaded at the linehaul destinations or other convenient locations, and transported to the depot, the destination of the backhaul deliveries. A comprehensive survey of algorithms and applications for the VRPB, including the VRPBTW, is given in (16). Following the classification scheme in (16), the AARP using Policy 1 can be viewed as two separated DARPs, one addressing the outbound trips and the other the inbound trips. The AARP using Policy 2 can be defined as a Vehicle Routing Problem with Simultaneous Delivery and Pickup and Time Windows (VRPSDPTW). The AARP using Policy 3 can be classified as a Vehicle Routing Problem with Clustered Backhauls and Time Windows (VRPCBTW). The VRPCBTW does not deal with pairing and precedence of service points, a crucial characteristic of the AARP.

Limited works in the literature address the specifics of the VRPBTW and its VRPSBTW and VRPCBTW variants. The VRPBTW has been formulated as a mixed integer linear program, but only relatively small instances can be solved to optimality. An exact solution approach for the VRPSBTW is presented in (17). Specifically, a column generation framework is proposed in which the problem is decomposed into a Master Problem (MP) and Subproblem (SP). The MP is formulated as a set covering problem and branch-and-price is proposed for solution of the SP. Solution of the SP supplies a feasible route for inclusion in the set of possible routes considered in the MP. The largest instance solved to optimality had 20 customers. Yano et al. (18) formulated the VRPCBTW as a set partitioning problem. They proposed an exact solution method based on branch-and-bound to generate optimal tours, each with a maximum of four linehaul and four backhaul customers. For the same problem with possibly more than four customers, Gelinas et al. (19) proposed an exact algorithm based on column generation for solving a similar set partitioning formulation of the VRPCBTW. The algorithm found optimal solutions for problems with up to 100 customers.

While promising, exact solution methods cannot be applied to typical problems of a size seen in real-world operations. Thus, numerous works have proposed heuristics for these problems. The majority of these heuristics include construction and improvement schemes based on classical greedy methods. More powerful methods have been proposed based on met heuristics. For example, Dethloff (20) proposed an extension of the cheapest insertion heuristic for the VRPSBTW. Thangiah et al. (21) proposed a heuristic for solution of the VRPCBTW. In the construction phase, the insertion procedure of Kontoravdis and Bard (22) proposed for the VRPTW is used to obtain initial solutions. Then, the initial solutions are improved through the application of λ-interchanges and 2-opt* exchanges in the improvement phase. Duhamel et al. (23) uses an insertion procedure proposed in (3) for initial solution construction, but proposed a tabu search heuristic for the improvement phase. An augmented objective function for the VRPCBTW is presented by Zhong and Cole (24), where violations of time windows, capacity and linehaul-backhaul precedence constraints are penalized. The cluster-first route-second method is used for initial route construction and intra- and inter-route operators are described for use in improving the tours. Metaheuristics, such as Tabu Search (23), genetic algorithms (25) and ant colony optimization (26), have also been proposed.

In the next section, a general formulation is presented that can be used to solve all three variants of the AARP. This formulation combines aspects of previously proposed formulations for the PDPTW and VRPBTW. It fills the need for a formulation of a PDPTW with linehaul and backhaul operations or the VRPCBTW with additional pairing and precedence constraints, i.e. AARP with Policy 3. The proposed formulation does not rely on a complete enumeration of the feasible tours, which is a requirement of the set partitioning formulation of the VRPCBTW and set covering approach for the VRPSBTW. The formulation given next includes additional constraints specific to an application involving passengers as opposed to cargo, including maximum passenger ride times and restrictions on idling with passengers onboard.

PROBLEM FORMULATION

In this section, the AARP is formulated. The formulation is preceded by the introduction of notation. Additional adaptations needed for different operational policy implementations are given.

Notation

The general formulation of the AARP builds on the existing formulations for the VRPBTW (16) and PDPTW (27).

The formulation is designed to be general and directly applicable for Policy 2. Small adaptations are required for the application of Policies 1 and 3 as described next.

FIGURE 2 Flowchart of Exact Solution Method

The procedure starts by feeding the LMP, modeled as a set covering problem, with a feasible solution consisting of a set of vehicles, each of which serves one request. The SP is a constrained shortest path problem. Solution of the SP produces a route with negative reduced cost. This route is added to the route set (or column set) used in the next iteration in which solution of the LMP is repeated. This process terminates when solution of the SP does not produce a route that is not already included in the column pool with negative reduced cost. With the final column pool (route set), the integer MP, a set partitioning problem, is solved. The route obtained from solution of the integer MP is reassembled through a proposed heuristic procedure to generate the final solution. Details associated with the MP, SP and Heuristic Reassemble procedure are provided next.

CP Model for SP

In the CP approach, each decision variable has a domain. For example, in the SP, the domain of each arc, xij, is {0, 1}. Similarly, the domain of load Li is {0, 1, …, Q}. Initially, the search space contains all combinations of the values in the domains of all decision variables. To avoid exploring the entire search space, CP first removes inconsistent values from the domains of the variables involved in each constraint. Then a search strategy (depth first, width first or multi-start) is applied to guide the search for a solution within the reduced search space. The search process can be viewed as traversing a tree, where the root is the starting point, a leaf node is a combination of values in the reduced search space and each branch represents a move (branching) within the search. A solution is a set of value assignments to the decision variables such that each variable is assigned to exactly one value from its domain. Together these values satisfy all constraints and minimize the objective function. Each leaf node is evaluated to determine if it will produce a feasible solution.

Two measures are suggested for speeding up the process of finding a feasible solution: 1) eliminate ineligible decision variable settings from the initial search space, wherein those decisions that include starting from the end depot, ending at the starting depot, self loops, or that would violate Constraints (13) – (15) are excluded, and 2) set branching limits for the route generation process. As mentioned in (28), in the context of column generation, optimality of the SP is only necessary to prove that no negative reduced cost routes exist in the last iteration, and feasible solutions to the SP are sufficient for preceding iterations. Thus, a lower branching limit (106) is used for these nonfinal iterations, while higher branching limits (108) are applied in the last iteration.

Heuristic Reassemble Procedure

The optimal solution to the LMP is obtained when there are no remaining routes with negative reduced cost to the SP. Unfortunately, this solution is not always integer-valued. A branching scheme was proposed in (10) to address this issue through adding additional arc flow constraints to the SP and resolving it. This process is repeated for each branching decision taken in the MP. The following observations are made:

The MP starts with a feasible solution in which one vehicle serves one request;
Each iteration generates a single unique route;
The newly generated routes that are selected by solution of the MP-SPP are always a subset of the newly generated routes that are selected by solution of the set covering problem.
The solution to the MP-SPP always includes one or more initial feasible routes.

Since solution from MP-SPP provides useful information, the following heuristic applies:

Step 1. Calculate the value of V = route cost/number of request served for each route selected by the MP-SPP.

Step 2. Select the route r with maximum V. Try to extract the first unvisited request on route r and insert it into the best feasible position on one of the other routes, r’. If this decreases the total cost, update r and r’, and go to Step 1. Otherwise, mark this request as visited and move to the next request in r. If all requests in r have been visited, stop.

Step 3. Repeat Step 1

HEURISTIC SOLUTION APRROACHES

Two heuristics proposed in the literature were modified for solution of the AARP. An overview of each is given first, followed by the modifications required to address the three variants of the AARP.

Jaw’s Heuristic

The first heuristic considered for solution to the AARP is the sequential insertion procedure originally proposed by Jaw (2) for the DARP problem. The algorithm processes each request in an unrouted request list (URL) in sequence, and assigns each request to a vehicle until the URL is exhausted. The main steps of Jaw’s sequential insertion procedure are summarized as follows:

Step 1: Sort URL by the requested pickup times in increasing order. Create a route from and back to the depot. Set r =1.

Step 2: Select the first unrouted request u from URL. Find all feasible insertion positions within all existing routes, 1 to r.

If a feasible insertion position is found, assign the request u to the route r* with minimum insertion cost, and update route r*.
If no feasible insertion position exists, create a new route from the depot to request u, and add a return to the depot. Set r = r+1.

Delete u from URL.

Step 3: Repeat step 2 until URL is empty.

The additional insertion cost to route r of inserting request u is calculated as the difference between the total cost of route r after the insertion minus its cost before the insertion. This is expressed in (29)

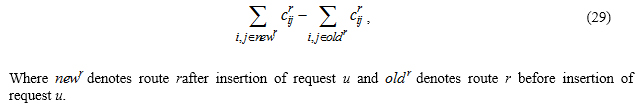
Solomon’s Insertion I1 Heuristic

The second heuristic considered here, Insertion I1 (I1), was proposed by Solomon (3) for the VRPTW. I1 constructs routes one at a time. For the first created route, a tour is developed from the depot to a “seed” request, which returns to the depot. Remaining requests are considered for insertion in the route. The cost of insertion of all remaining unrouted requests is computed. The request with the minimum insertion cost that can be feasibly inserted is selected. Insertion of additional requests is considered until no remaining unrouted request can be feasibly inserted. A new route is then created. The process is repeated until all requests have been included in a tour. At each iteration in which a new route is created, the remaining unrouted request with the minimum value of , 0≤ ≤1, for outbound trips and for inbound trips is selected as the seed. Trips that are far from the depot and have an earlier deadline are, thus, favored in choosing the request.

The main steps of I1 can now be summarized:

Step 1: Initialize r = 0.

Step 2: Set r = r+1. Select the ‘seed’ request u* with the minimum value of from URL for inclusion in route r. Add u* to route r and delete it from URL. If URL is empty, stop.

Step 3: For each remaining unrouted request u in URL, find the feasible insertion position in route r, if a feasible insertion exists, that minimizes the additional insertion cost (equation (30)).

If a feasible insertion exists, select request u* with the minimum additional insertion cost (equation (30)), and insert this request at its best feasible insertion position in route r. Update route r, and delete u* from URL. If there is no feasible insertion of any unrouted request in route r, go to step 2.

Step 4: Repeat step 3 until URL is empty.

The two heuristics are quite similar, but differ in one fundamental aspect relating to the choice of a feasible insertion position for the unrouted requests. In Jaw’s heuristic, for each selected unrouted request u, its best insertion position within all constructed routes is evaluated and the insertion is made accordingly. When a request cannot be feasibly inserted in any existing route, a new route is constructed. The request is inserted in the new route. The next unrouted request from a list that was not yet tested will be considered for inclusion in this expanded set of constructed routes. In I1 this evaluation is conducted over only the most recently constructed route. The list of unrouted requests must be considered and any possible insertions must be made in that route before considering insertion in another route.

Both heuristics as described can be used directly on the AARP with Policies 1 and 2. For Policy 3, however, feasibility is further restricted by outbound and inbound trip separation requirements. Both heuristics can be adapted to deal with this additional constraint. Specifically, modifications are made when choosing the best feasible insertion position for each unrouted request: if the selected unrouted request u is an outbound trip, its dropoff location must be inserted before the pickup of the first inbound trip, given that there are inbound trips in the current route. Likewise, if the unrouted request u is an inbound trip, its pickup location must be inserted after the dropoff location of the last outbound trip, assuming there is an outbound trip in the current route.

Checking Solution Feasibility

Both heuristics ensure that the problem constraints associated with time windows, precedence and pairing, maximum ride time, shift duration for drivers and vehicle capacities are satisfied during the insertion process. An insertion of a request in a route is feasible only if it does not lead to violation of any of these constraints by inclusion of this request. Moreover, its inclusion should not create other violations of these constraints for other requests already included in the route. The implementation of these constraints during this process is important and is described next.

Time Window Constraints. Time window feasibility is maintained in a route if the insertion of a new request does not push the vehicle arrival time at any node i past its latest service time li. While a vehicle without a passenger onboard is permitted to arrive at a pickup node earlier than its earliest service time ei, thus incurring an additional waiting cost, no vehicle is permitted to idle while carrying passengers. The procedure proposed in (2) is applied for the calculations of earliest service time, ei, and latest service time, li.

To ensure that time window constraints are met, we must check that ei and li fall within each request’s time window for each i in the route and for requests considered for inclusion.

Precedence and Pairing Constraints. For any insertion of a new request, precedence and pairing constraints are ensured by simultaneously inserting both the pickup and dropoff locations associated with a single request within the route. The pickup location must precede the dropoff location.

Maximum Ride Time Constraints.For each considered insertion of a request, the insertion must not cause a violation in constraints (17), whether directly for the request or for other requests already inserted in the route. The maximum ride time Ri is a function of direct (shortest path) ride time DRTi. Herein, a piecewise linear function (30) is applied:

Shift Duration Limit for Drivers. Any insertion of a new request cannot extend the route duration over the shift duration limit for a driver, as expressed by constraints (16). Thus, shift duration must be assessed for each insertion of a request.

Vehicle Capacity Constraints. Any insertion of a new request must adhere to capacity constraints (13). Thus, no insertion is made if its inclusion will cause the vehicle to exceed its capacity. This must be assessed at each potential insertion location, because the number of requests handled at any point in time changes over the route duration.

NUMERICAL EXPERIMENTS

Experiment Design

To investigate the efficiency of the proposed solution approach, the solution methods are tested on a real-world problem instance. The test case involves service records for one service day in January of 2012 out of Washington Dulles International Airport (IAD). It includes 164 outbound requests involving 212 passengers and 22 inbound requests involving 41 passengers. For each request, detailed information, including desired pickup time, number of passengers, latitude and longitude of pickup and dropoff locations, and assigned vehicle index are also included. All requests were served by a fleet of identical vehicles. FIGURE 3 shows the partial distributions of the requested pickup (inbound) and dropoff (outbound) locations. The service area covers Maryland, District of Columbia, Virginia and Pennsylvania. Distances and travel times between pairs of customer locations were calculated through the OD Cost Matrix Tool in the Network Analyst toolbox of ArcGIS. The travel time is computed based on the shortest distance and speed limits.

Parameters of the model and the algorithms are presented in TABLE 1. The solution methods were implemented in Visual C++ 2010 and run on a personal computer with Intel(R) CPU 3.10GHz and 4.0GB RAM. The SP associated with the exact solution method was solved by the C++ Concert Technology of CP (Constraint Programming) solver in the IBM-ILOG CPLEX.

Algorithm Performance

The CPCG approach was tested on cases with 10, 20 and 30 requests under the most general policy, Policy 2. Computational time increases exponentially with increasing number of customers. Thus, solution of problem instances with significantly more than 30 customers is precluded. The results are compared with those obtained through the adapted Jaw’s algorithm in TABLE 2. The numbers in parentheses are outbound and inbound requests, respectively. Results show that the maximum gap between the exact solution and the adapted Jaw’s algorithm is approximately 7% (with 20 requests), but the computational time is around 1/1200 of that of CPCG.

Policy Performance

Computational results obtained by applying the two heuristics for each of the three operational policies are shown in TABLE 3. From TABLE 3, two significant conclusions can be reached. First, Jaw’s heuristic outperforms I1. For all three policies, the computation time required by Jaw’s heuristic is only between 14 and 25% of that required by I1. The longer I1 computation time can be explained by the requirement for assessing the insertion of every unrouted request when each route is constructed. For each of the three operational policies, the total cost of the routes built through Jaw’s heuristic is below that developed by I1. This may be due to the ‘seed’ selection process of I1, where the furthest unrouted request is selected for inclusion. The long distance to this request may lead to longer empty vehicle miles, and thus, increased route duration and total cost.

Second, both heuristics reveal that Policy 2 provides the best performance in terms of number of needed vehicles, idle time, empty/loaded driving time or miles traveled, and total cost, Policy 3 the second best performance, and Policy 1 the worst performance. That Policy 2 provides the best performance is unsurprising and can be shown theoretically, because it is the least constrained of the three variants. From run results of Jaw’s heuristic, Policy 2 requires the fewest vehicles, lowest idle time, lowest empty vehicle miles, and lowest total cost of the three policies. Accordingly, Policy 2 has the highest vehicle utilization rate of the three. The vehicle utilization rate of Policy 3 is significantly above that of Policy 1, but below that of Policy 2. This difference in vehicle utilization rate is caused by requirements for ordering outbound and inbound operations with Policies 1 and 3.

To assess the value of this optimization-based approach, solutions obtained from the heuristics were compared against manually derived routes used to deploy the vehicle fleet on the date of the case study. In actual operations on the date of service, Policy 2 was employed. From records maintained for this date, 37 vehicles were employed. Stringing the vehicle routes together where feasible would permit completion by as few as 28 vehicles. Many of the routes did not comply with maximum ride time constraints and several violated constraints that prohibit waiting with a passenger onboard. Of course, violations were addressed during actual operations. In comparison, results from the proposed heuristic for the AARP under Policy 2 required only 17 vehicles to serve the same requests. This is an approximately 60% improvement in vehicle utilization.

CONCLUSIONS AND FUTURE WORK

The AARP is formulated here as a mixed integer program. Three implementations corresponding to three different operational policies under consideration in practice are investigated. Exact and heuristic solution procedures are proposed. The performance of the proposed solution approaches is compared in a case study involving data from one day’s operation of an actual service provider. No exact solution could be obtained for the full-version of the case study, but an exact solution was obtained for a reduced version with 30 customer requests. In a comparison the results of the adapted Jaw’s algorithm were within 7% of the exact solution and required only 1/1200 the computation time. In the original case study, the adapted Jaw’s algorithm outperformed the second proposed heuristic. Thus, the heuristic is an effective and efficient approach for addressing the AARP, yielding significantly better results than routes and schedules determined manually.

The proposed methodologies are also relevant for other routing and scheduling applications involving ‘one-to-many-to-one’ operations, such as passenger feeder problems involving “subscription services,” school bus routing, carpooling, and express collection and delivery. Other possible applications arise in reverse logistics operations, including the delivery of full and collection of empty bottles between a manufacture and retailers. However, the reverse logistics problem is simpler than the airport shuttle, because the goods to be transported are identical. Thus, every unit to be picked up can equally satisfy customer demand.

While the heuristics described herein provide good results with low computational effort, more sophisticated heuristics may provide improved solutions. Both described heuristics are construction heuristics. Thus, constructed routes can be improved through the application of improvement operators, such as λ-interchange, 2-opt* exchange, trip exchange and trip reinsertion. A cluster-first route-second methodology may also address this myopic nature. Clustering can be based on both temporal and spatial characteristics of the pickup and drop-off locations. The authors are currently investigating these and other improvements.

In a dynamic setting, new requests may be received on short notice while some vehicles are en route. The operator must quickly insert these new requests within previously constructed routes and schedules. In the airport operations of the case study, most inbound requests are known in advance, but almost all outbound trips arise dynamically. A fast algorithm to find a good feasible insertion for the new requests is required. The authors are working to extend the developed model and solution methodologies to operations with uncertainties in travel and service times, as well as dynamic requests.

ACKNOWLEDGEMENTS

This work was funded by the Maryland Industrial Partnership (MIPS) and IT Curves. This support is gratefully acknowledged, but implies no endorsements of the findings.

REFERENCES

Junker, U., S.E. Karisch, N. Kohl, et al. A Framework for Constraint Programming Based Column Generation. in Principles and Practice of Constraint Programming–CP’99. Springer.
Jaw, J.J., A.R. Odoni, H.N. Psaraftis, et al., A Heuristic Algorithm for the Multivehicle Advance Request Dial-a-Ride Problem with Time Windows. Transportation Research Part B-Methodological, 20(3), 1986. pp. 243-257.
Solomon, M.M., Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Operations Research, 35(2), 1987. pp. 254-265.
Kolen, A.W., A.R. Kan, and H. Trienekens, Vehicle Routing with Time Windows. Operations Research, 35(2), 1987. pp. 266-273.
Dantzig, G.B. and J.H. Ramser, The Truck Dispatching Problem. Management Science, 6(1), 1959. pp. 80-91.
Desrochers, M., J. Desrosiers, and M. Solomon, A New Optimization Algorithm for the Vehicle Routing Problem with Time Windows. Operations Research, 40(2), 1992. pp. 342-354.
Prescott-Gagnon, E., G. Desaulniers, and L.M. Rousseau, A Branch-and-Price-Based Large Neighborhood Search Algorithm for the Vehicle Routing Problem with Time Windows. Networks, 54(4), 2009. pp. 190-204.
Braysy, I. and M. Gendreau, Vehicle Routing Problem with Time Windows, Part I: Route Construction and Local Search Algorithms. Transportation Science, 39(1), 2005. pp. 104-118.
Braysy, I. and M. Gendreau, Vehicle Routing Problem with Time Windows, Part Ii: Metaheuristics. Transportation Science, 39(1), 2005. pp. 119-139.
Dumas, Y., J. Desrosiers, and F. Soumis, The Pickup and Delivery Problem with Time Windows. European Journal of Operational Research, 54(1), 1991. pp. 7-22.
Wallace, N.E., Optimization in Dial-a-Ride System Analysis: A Comparison of Recent Modelling and an Expected Value Model, 1978.
Cordeau, J.F. and G. Laporte, The Dial-a-Ride Problem: Models and Algorithms. Annals of Operations Research, 153(1), 2007. pp. 29-46.
Parragh, S., K. Doerner, and R. Hartl, A Survey on Pickup and Delivery Problems Part Ii: Transportation between Pickup and Delivery Locations. Journal für Betriebswirtschaft, 58(2), 2008. pp. 81-117.
Berbeglia, G., J.F. Cordeau, I. Gribkovskaia, et al., Static Pickup and Delivery Problems: A Classification Scheme and Survey. Top, 15(1), 2007. pp. 1-31.
Gribkovskaia, I. and G. Laporte, One-to-Many-to-One Single Vehicle Pickup and Delivery Problems in the Vehicle Routing Problem: Latest Advances and New Challenges, B. Golden, S. Raghavan, and E. Wasil, Editors. 2008, Springer US. p. 359-377.
Parragh, S., K. Doerner, and R. Hartl, A Survey on Pickup and Delivery Problems Part I: Transportation between Customers and Depot. Journal für Betriebswirtschaft, 58(1), 2008. pp. 21-51.
Angelelli, E. and R. Mansini, The Vehicle Routing Problem with Time Windows and Simultaneous Pick-up and Delivery. Quantitative approaches to distribution logistics and supply chain management, 2002. pp. 249-267.
Yano, C.A., T.J. Chan, L.K. Richter, et al., Vehicle Routing at Quality Stores. Interfaces, 17(2), 1987. pp. 52-63.
Gélinas, S., M. Desrochers, J. Desrosiers, et al., A New Branching Strategy for Time Constrained Routing Problems with Application to Backhauling. Annals of Operations Research, 61(1), 1995. pp. 91-109.
Dethloff, J., Vehicle Routing and Reverse Logistics: The Vehicle Routing Problem with Simultaneous Delivery and Pick-Up. Or Spektrum, 23(1), 2001. pp. 79-96.
Thangiah, S.R., J.Y. Potvin, and T. Sun, Heuristic Approaches to Vehicle Routing with Backhauls and Time Windows. Computers & Operations Research, 23(11), 1996. pp. 1043-1057.
Kontoravdis, G. and J.F. Bard, A Grasp for the Vehicle Routing Problem with Time Windows. ORSA journal on Computing, 7(1), 1995. pp. 10-23.
Duhamel, C., J.-Y. Potvin, and J.-M. Rousseau, A Tabu Search Heuristic for the Vehicle Routing Problem with Backhauls and Time Windows. Transportation Science, 31(1), 1997. pp. 49-59.
Zhong, Y. and M.H. Cole, A Vehicle Routing Problem with Backhauls and Time Windows: A Guided Local Search Solution. Transportation Research Part E: Logistics and Transportation Review, 41(2), 2005. pp. 131-144.
Tasan, A.S. and M. Gen, A Genetic Algorithm Based Approach to Vehicle Routing Problem with Simultaneous Pick-up and Deliveries. Computers & Industrial Engineering, 62(3), 2012. pp. 755-761.
Paraphantakul, C., E. Miller-Hooks, and S. Opasanon, Scheduling Deliveries with Backhauls in Thailand’s Cement Industry. Transportation Research Record, (2269), 2012. pp. 73-82.
Ropke, S. and J.F. Cordeau, Branch and Cut and Price for the Pickup and Delivery Problem with Time Windows. Transportation Science, 43(3), 2009. pp. 267-286.
Irnich, S. and G. Desaulniers, Shortest Path Problems with Resource Constraints, in Column Generation, G. Desaulniers, J. Desrosiers, and M.M. Solomon, Editors. 2005, Springer: New York. p. 33-65.